Introduction to Graph in Programming

Graphs what are they? a graph is a data structure made up of nodes or in other terms vertices and edges or the connection between nodes.

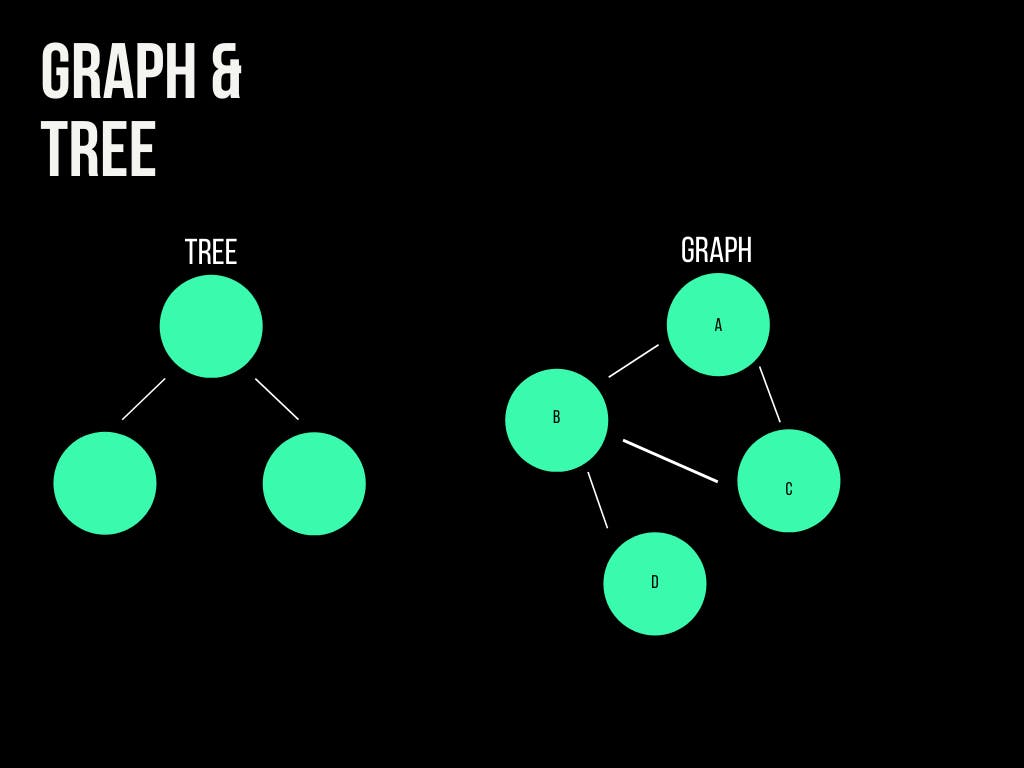
When we view graphs in a depiction it will be typically represented by circles and edges as lines between the circles.

a graph can have any number of root elements and have multiple paths between its nodes, unlike trees which is a kind of graph with only one root and only one unique path between nodes.

Each node is a structure that may contain information like person id, name, gender, and locale.

The two most commonly used representations of a graph are...

1. Adjacency Matrix
2. Adjacency List

Adjacency Matrix

An adjacency matrix is a square matrix used to represent a finite graph. The elements of the matrix indicate whether pairs of vertices are adjacent or not in the graph.

Code Example

// each row is a node
// 1 = connections
const vertices = ["A", "B", "C", "D", "E"];

const adjacencyMatrix = [
  [0, 1, 0, 1, 0],
  [1, 0, 1, 0, 0],
  [0, 1, 1, 1, 1],
  [1, 0, 1, 0, 1],
  [0, 0, 1, 1, 0,]
];

Adjacency List

An adjacency list is a collection of unordered lists used to represent a finite graph. Each unordered list within an adjacency list describes the set of neighbors of a particular vertex in the graph. This is one of several commonly used representations of graphs for use in computer programs.

Code Example

// Adjacency list as a Hashmap
const graph = {
  a: ['a', 'b'],
  b: ['c'],
  c: ['d'],
  d: ['b', 'c']
}

Time Complexity

The following table gives the time complexity cost of performing various operations on graphs, for each of these representations, with |V| the number of vertices and |E| the number of edges.

Graphs no doubt come up in technical interviews quite often, if you're looking for a career in tech, then start learning more about graphs today.

Thanks for reading, Cheers!